// ホーム / 資料 / 分布関数の世界 / 一様分布（離散）

一様分布（離散）(Discrete uniform distribution)

ギャンブルに勝つ！一様分布（離散）

どの教科書でもまず間違いなく最初に挙げる確率の事例といえば、やっぱりサイコロじゃないでしょうか（ベルヌーイ分布よりも確率っぽい）。
6面体のサイコロをふって、1の出る確率は？じゃあ偶数の出る確率は？などなど聞き覚えがあるでしょう。
ここで現れる重要なキーワードは「同様に確からしい」。 つまり、1が出る確率も6が出る確率も同じということ。したがって、どの目が出る確率もみんな 1/6 となるのです（確率を全部足したら 1 にならないといけないからね）。これこそが一様分布の一様（全て同じ）たる所以ですね。
グラフにするとこんな感じ。
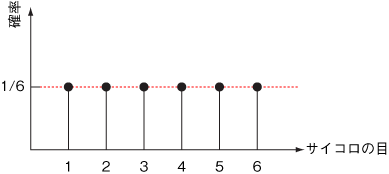
例えば、ルーレットも代表的な一様分布の事例。みんな知っている通り、円盤の円周を等間隔に区切って、転がしたボールがどの区間に落ちるかを当てるゲームですね。 この場合も、どの目が出るか（どこにボールが落ちるか）は「同様に確からしい」ので、一様分布になります。
ちなみに、実際のルーレットの区画の数は 37（ヨーロピアンスタイル）、38（アメリカンスタイル）、39（メキシカンスタイル）の3種類あったりします。ちょっと得したでしょ？

サイコロにしても、ルーレットにしても確率的に発生する事象は番号がつけられます（サイコロなら目そのもの。ルーレットなら、適当な区画から順に番号をつければいいですね）。 また、必ず上限と下限があります。番号の最小値をa、最大値をbとすると、どの目が出る確率も、
\frac{1}{b-a+1}
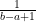となります（分母の +1 に注意！植木算をがんばって思い出してください）。サイコロならば 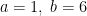a=1,\;b=6 ですね。


特別な条件下の一様分布には特別な名前が付いているものです。
  • 公正なコイン（裏表のどちらが出るかが同様に確からしいコイン）を使ったコイントスで、表を 1、裏を 0 としたもの。これは成功確率が0.5のベルヌーイ分布と一致します。
  • 目が1つしかない場合（2枚のコインを張り合わせて、両面表にしたコインでの表の出る確率）も考えられます（いや、面白いかじゃなくてあくまで可能性ですから！）。この分布は退化分布と呼ばれています。
もうひとつの特別な状況が連続極限で、その場合は一様分布（連続）となります。

分布の形状

基本情報

  • 2つのパラメータ a,b が必要です。
    a <b

    これらのパラメータはそれぞれ、分布の最小値と最大値を表します。

  • 整数 x=\{a, a+1, \cdots, b\} で定義された離散分布です。

確率

  • 累積分布関数
    F(x)=\begin{cases}0\;&(x<a)\\\frac{x-a+1}{b-a+1}\;&(x=\{a,a+1,\cdots,b\})\\1\;&(x>b)\end{cases}
  • 確率質量関数
    f(x)=\begin{cases}\frac{1}{b-a+1}\;&(x=\{a,a+1,\cdots,b\})\\0\;&(\text{otherwise})\end{cases}
  • Excel での累積分布関数 (c.d.f.) と 確率質量関数 (p.m.f.)の求め方
     
    1
    2
    3
    4
    5
    6
       
    7
       
    AB
    データ説明
    3 対象となる値
    1 分布のパラメータ A の値
    6 分布のパラメータ B の値
    数式説明（計算結果）
    =IF(A2<A3,0,IF(A2<=A4, (A2-A3+1)/(A4-A3+1),1)) 上のデータに対する累積分布関数の値
    =IF(AND(A3<=A2,A2<=A4),1/(A4-A3+1), 0) 上のデータに対する確率質量関数の値

分布の特徴

平均 – 分布の”中心”はどこ？ (定義)

  • 分布の平均 は次式で与えられます。
    \frac{a+b}{2}
  • Excel での計算法
     
    1
    2
    3
    4
    5
    AB
    データ説明
    1 分布のパラメータ A の値
    6 分布のパラメータ B の値
    数式説明（計算結果）
    =(A2+A3)/2 上のデータに対する分布の平均

標準偏差 – 分布はどのくらい広がっているか（定義）

  • 分布の分散 は次式で与えられます。
    \frac{(b-a+1)^2-1}{12}

    標準偏差 は 分散の正の平方根です。

  • Excel での計算法
     
    1
    2
    3
    4
    5
    AB
    データ説明
    1 分布のパラメータ A の値
    6 分布のパラメータ B の値
    数式説明（計算結果）
    =SQRT(((A3-A2+1)^2-1)/12) 上のデータに対する分布の標準偏差

歪度 – 分布はどちらに偏っているか(定義)

  • 分布の歪度 は 0 です。

尖度 – 尖っているか丸まっているか (定義)

  • 分布の尖度 は次式で与えられます。
    -\frac{6((b-a+1)^2+1}{5((b-a+1)^2-1}
  • Excel での計算法
     
    1
    2
    3
    4
    5
    AB
    データ説明
    1 分布のパラメータ A の値
    6 分布のパラメータ B の値
    数式説明（計算結果）
    =-6*((A3-A2+1)^2+1)/(5*((A3-A2+1)^2-1)) 上のデータに対する分布の尖度

乱数

  • Excel での乱数生成法
     
    1
    2
    3
    4
    5
       
    AB
    データ説明
    1 分布のパラメータ A の値
    6 分布のパラメータ B の値
    数式説明（計算結果）
    =INT((A3-A2+1)*NTRAND(100))+A2 100個の一様乱数を Mersenne Twister アルゴリズムで生成します。

    メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A5:A104 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

参照

 

Comments are closed.