Jul 17, 2012
2人が同時に好きな自然数を叫びます。
A:「10」
B:「132」
この2つの数字はどちらも2で割り切れます。難しい言葉で言うと「この2つの数字の公約数は2」ということです(小学校で習うんだったかな)。
ではもう一度
A:「65」
B:「154」
この2つの場合はどうでしょう。すぐに分かりますがこの2つの数字には公約数はありません。難しい言葉でいうと「この2つの数字は互いに素」ということです。
ではここで問題「任意に2つの数字が互いに素である確率は?」
ちょっと実験してみようにもこれはなかなか難しいです。
というのも、任意の自然数ですから、10とか250とかはもちろん
20482093840734198720491209341412987461298402971029347019823740194
や
93410974246817469817648164815451276453725653666635467341618253600027
みたいのでもいいですし、、、というか、こういう数字も公平に出てこないと実験になりません。
さあ数字を言え!といってこんな数字を挙げられる人はいないでしょう。
じゃあコンピューターで、といっても無限にある自然数をすべて公平に挙げるのは無理でしょう。
しかし人間の知性に限界はありません。この問題を理論的に解きましょう。
例えば、8と16の公約数は2、4、8となりますが、互いに素かどうかを見るには素数の公約数だけみればいいということに注目します。
この例なら4で割れるかどうかを調べはしません。素数2で割れるかを見るだけです。
15と105なら素数3で割れます。
8と105なら素数2、素数3、素数5、素数7…と素数を順に調べてどの素数も共通の公約数になっていない、つまり互いに素だと分かります。
任意の自然数 が素数
が素数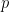 で割れる確率は、
で割れる確率は、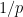 であるというのは分かりますか?
であるというのは分かりますか?
例えば、素数3で割れる数というのは となります。つまり全自然数の3つに1つが素数3で割れる自然数だということになります。
パッと選んだ自然数が3で割れるかは3つに1つ、つまり確率1/3となります。
となります。つまり全自然数の3つに1つが素数3で割れる自然数だということになります。
パッと選んだ自然数が3で割れるかは3つに1つ、つまり確率1/3となります。
同様に素数5で割れる確率は1/5、素数13で割れる確率は1/13、、、素数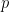 で割れる確率は
で割れる確率は となります。
となります。
従って自然数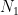 と
と がどちらも素数
がどちらも素数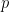 で割れる確率は
で割れる確率は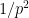 となります。
となります。
ということは自然数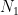 と
と が素数
が素数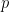 を公約数に持たない確率は
を公約数に持たない確率は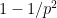 となります。
となります。
自然数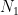 と
と が互いに素ということはあらゆる素数が公約数でないということなので、その確率は
が互いに素ということはあらゆる素数が公約数でないということなので、その確率は

です。なんとも複雑そうな式ですが、この値は幾らになるでしょうか?
結論だけ言うと、
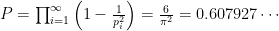
です。なんとこんなところに円周率が出てきます!
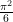 という部分は「バーゼル問題」という数学の歴史的難問(解決に100年!)に端を発し、数学の最大の未解決問題とされる「リーマン予想」にも関わるネタで、
とてもここでは書ききれません。
という部分は「バーゼル問題」という数学の歴史的難問(解決に100年!)に端を発し、数学の最大の未解決問題とされる「リーマン予想」にも関わるネタで、
とてもここでは書ききれません。
Feb 09, 2012
火星に生物はいるだろうか?生物のいる確率はどのくらいだろうか?順を追って求めてみよう。
まずは火星に人間がいる確率を としよう。例えば…
としよう。例えば… くらいかな。
くらいかな。
よし、次に火星に犬がいる確率を としよう。なんとなく犬は人間よりいそうなんで、
としよう。なんとなく犬は人間よりいそうなんで、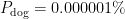 とでもしてみるか。
とでもしてみるか。
どんどん続けよう。次に火星にアメンボがいる確率を としよう。これはきっと人間なんかよりずーっといる確率が高いだろう。よし
としよう。これはきっと人間なんかよりずーっといる確率が高いだろう。よし だ。
だ。
ここで中間報告。では、火星に人間も犬もアメンボもいない確率はいくつになるだろうか。それは、”(人間がいない)かつ(犬がいない)かつ(アメンボがいない)”確率となるので、次式で与えられる。
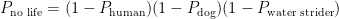

なるほど…しかし、まだ他にも調査すべき生物はたくさんある!象がいる確率、マントヒヒがいる確率、ムカデがいる確率、カピバラがいる確率…どれもきっと確率は0ではないだろう。
ある生物がいる確率を とする。
とする。 は生物の種別を表していている。ものの本によると生物は1億種という説もある。それらが火星にいる確率が平均して
は生物の種別を表していている。ものの本によると生物は1億種という説もある。それらが火星にいる確率が平均して とすると、火星にまったく生物がいない確率は、
とすると、火星にまったく生物がいない確率は、

となる。ちょっと待てよ、、、ということは、火星に何か生物がいる確率は、

これは驚いた!火星にはきっと何かいるぞ!
上記の推論はどこがおかしいか分かりますが?
Dec 20, 2011
「二人の子供問題」という有名な確率のトピックです。
昼休み。食事も終えて、職場の仲間とまったりとコーヒーを飲んでいます。誰ともなしに家族の話題になりました。
独りモノのあなたな職場の仲間Aさんにこんな質問をしました。
では、ここで問題
あなたはAさんに更に質問をぶつけました。
なるほど。では、ここで問題
もう一人Bさんが隣に座っています。Bさんは今日はたまたま子供を連れてきています。男の子です。
あなたはBさんにも質問をしました。
ふーむ、、、ここで問題
問2と問3の違いが分かりますか?AさんもBさんも二人子供がいて、少なくとも一人は男の子であることが分かっています。
ちなみに解答は(男の子が生まれる確率と女の子が生まれる確率は等しいとしましょう)
です。
Dec 20, 2011
確率のネタではないですが、小話をひとつ
NtRandでは”Mersenne-Twister”と呼ばれる一様乱数生成アルゴリズムが採用されています。
このアルゴリズムで生成される乱数は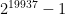 、実に6002桁という途方もない長い周期をもっています。
、実に6002桁という途方もない長い周期をもっています。
さて、この数は”メルセンヌ素数”と呼ばれる一群の数字のうちの一つで、これが”Mersenne-Twister”の語源になっています。
メルセンヌ素数とは、素数のうちで という形で書けるもののことです。
つまりMarsenne-Twisterの周期は
という形で書けるもののことです。
つまりMarsenne-Twisterの周期は のメルセンヌ素数です。
2001年5月現在、メルセンヌ素数は47個見つかっています。
のメルセンヌ素数です。
2001年5月現在、メルセンヌ素数は47個見つかっています。 のメルセンヌ素数は24番目のものです。
のメルセンヌ素数は24番目のものです。
1644年、マラン・メルセンヌさんが  がメルセンヌ素数であると主張しました。
残念なことに彼は
がメルセンヌ素数であると主張しました。
残念なことに彼は を見逃していました。
を見逃していました。
更に残念なことに、、、
1903年、アメリカで行われた数学会でフランク・ネルソン・コールなる人物が発表のため登壇しました。タイトルは「大きな数の素因数分解」。
彼はまず黒板に を書き下しました。
を書き下しました。
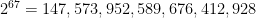
そこから1を引き、そして次に

の計算を行いました。その結果は、、、 !
その間彼は一言も口をきかず、静かに席に戻りました。その後会場は万雷の拍手が沸いたそうです。
!
その間彼は一言も口をきかず、静かに席に戻りました。その後会場は万雷の拍手が沸いたそうです。
メルセンヌさんの主張から250年以上経って、 が素数でないことが分かったのです。
が素数でないことが分かったのです。
今では も素数ではないことが分かっています。
も素数ではないことが分かっています。
May 25, 2010
某国、華やかなカジノの街。
ルーレット、スロットマシーン、カード…有象無象どもが一攫千金を目論んで目を血走らせて必死にもがいている。
さて今日はどのゲームでひと稼ぎしようか…ふと片隅にあるゲームに目がとまる。
「サイコロを転がして出た目が1なら1円、2なら2円…出た目と同じ額を賞金として進呈!」
なんとも幼稚なギャンブルだが、まぁいいや。ちょっとやってみるか。
参加費用は4円か。サイコロなんだから5か6を出せばもうかるじゃないか、チョロイチョロイ。
…1時間後…
すっかりスッカラカンになった彼は道端でボロ雑巾のようになっていた。
もちろん、確率を熟知したあなたはこのゲームには参加しないはずですね。
そう、期待値の問題です。このゲームの賞金の期待値

は、
です。賞金は 3.5円しか期待できないのに参加費が4円。長い目でみるとどんどんと負けが込んでいくのです(ちなみに1枚300円の宝くじの期待値は大体142円だそうです)。
リベンジだとばかりに再びカジノにやってきた彼。今度は確率の勉強もしっかりしてきた。
うーん、どのゲームも期待値を計算するとマイナスのものばかりか(当たり前。ギャンブルは胴元が儲かるようになっている)…なまじ確率の勉強をしたのでどのゲームも割に合わないと感じてしまうなぁ。
ふと片隅にあるゲームに目がとまる。
「コイントスゲーム!外れなし!表が出たら賞金は倍!!ただし裏が出たらゲームオーバー」
つまり、
- 1回目で裏が出たら賞金1円
- 2回目で裏が出たら賞金2円
- 3回目で裏が出たら賞金4円
- 4回目で裏が出たら賞金8円
- (以下賞金は倍々)
なるほど面白そうだ。おっといけない、軽々に飛びついては痛い目に逢う。まずは期待値を計算してみよう。
各パターンの確率は、
- 裏:

- 表裏:

- 表表裏:

- 表表表裏:
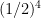
- 表表表表裏:

- (あとは分かるでしょう)
となるので、期待値は
こりゃ凄い、何と
期待値は無限大だ!幾らでも儲かるってことか!!で、参加費はいくらだって?1億円か。安い安い!!よ~し、やるぞ!!!…はたして彼の運命やいかに…
どうです?あなたはこのゲームに参加しますか?参加費100円でもやらないのではないでしょうか?(ちなみに100円以上の賞金を手にするには、7回連続して表を出す必要があります)。
でも確かに期待値は無限大…腑に落ちませんね。これが「サンクトペテルブルグのパラドックス」です。
May 24, 2010
モンテカルロシミュレーションの第1歩として、100パーセントどの教科書にも載っている例題があります。
どの教科書にも載っていて、このサイトに無いのも悔しいので載せておきます。
一様乱数から円周率を求めよう
1辺が1の正方形を用意します。そこに4分の1円を描いておきます。この正方形内に一様に点を打っていき、
(円内の点の数)/(全点の数)を計算すると、
これは
(4分の1円面積)/(正方形の面積)に近づいていきます。
(4分の1円面積)/(正方形の面積)はすなわち
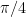
なので、(円内の点の数)×4 /(全点の数)は円周率
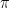
に近づいていきます。
May 19, 2010
モテモテで我が世の春を謳歌していたあなたは、いよいよ真剣に結婚を考えることにしました。しかし焦って貧乏くじを引きたくない!できるだけいい条件の人と結婚したい!
あなたは勝負はこの1年と決めて、ある結婚相談所に登録することにしました。そこはかなり値段が張るだけはあって「今後1年で100人のお相手の紹介を保証」とのこと。ただし…
- (1) 前もって相手のプロフィールなどは見せられない(条件などは会うまで分からない)
- (2) 1度に1人しか会えない
- (3) 交際を断った場合に次の人を紹介する
- (4) 一度断った相手とは二度と会えない(キープは不可)
- (5) こちらが OK すれば相手は必ず応じる。そしてゴールイン!
という条件付きです。
この人だ!と思ってももしかしたら次にもっといい人が現れるかも…でもそうこうしているうちに1番の人を見逃してしまっているかも…これは綿密なる戦略が必要だ!
そこであなたは先ず勇気を出して最初の何人かを見逃して(観察して)、その後「これまでに見逃した人より高条件の人」が現れたら問答無用でその人をゲットする、という戦略を採用することにしました。
この戦略だと、見逃す人数が少なすぎると、高条件の人を見逃す確率は減るけども低条件の人を選んでしまう確率も増える。見逃す人が多すぎると、最高条件の人を見逃してしまうかもしれない…では何人を見逃すことで最高の相手をゲットする確率が一番高くなるでしょうか?
結論を先に言うと、最初の37人を見逃すのが最良の戦略で、その場合最高の相手をゲットする確率は約37.1%となります。
ここから先は数学の話

人の見合い相手(今の例では

)のうち、見逃す人数を

とする。
本当の No.1 の相手が

番目にいる場合で、しかもその人を選ぶ確率を
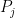
と書くとしよう。
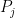
を考えてみよう。これは
(j 番目に最高の相手がいる確率)×(そこに達する確率)
と定義される。
前者の確率は

となる(完全にデタラメなので
一様分布)。
後者の確率は、運命の j 番目の相手に至るまでに出会う(j-1)人のうちの最高の人が、最初の s 人に含まれていればいいというのは分かるだろうか?
もし(j-1)人のうちの最高の人が最初の s 人に含まれていなければその人に出会った時点で婚活は終了し、運命の人には出会えないことになるからである。
逆にこの人が最初の s 人に含まれていれば、観察期間が終了して運命の j 番目の相手に出会うまでは見逃した人より高条件の人には出会わないことになる。
というわけで、後者の確率は
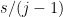
である。結局
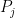
は、
となる(j が 1 から s までの場合は最高の人を見逃してしまった!ということで出逢う確率は 0)。
最高の相手に出会う確率は
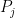
の和、つまり
となる。あとはこれを最大にする

を見つければよいことになる!
ちなみにこの 37% という何ともキレの悪い数字は一体何かというと、
です。何とこんなところに
自然対数の底 
が!!
May 18, 2010
この一様乱数(連続)を利用したゲームは
http://beetama.blog14.fc2.com/blog-date-200807.html
に掲載されていたものを参考にしました。ペコリ。
ルール
1箇所に赤い丸印(基準点)がつけてあるリングがあります。リングの任意の2箇所にボタンを使って切り込みを入れます。その結果リングは2つに分割されますが、そのうち
赤い丸印がない方があなたの取り分、もう一方が闇のオーナーの取り分となります。

- あなたの取り分が大きい場合:あなたの勝利。闇のオーナーとの取り分の差額が手に入る。
- あなたの取り分が小さい場合:あなたの負け。闇のオーナーとの取り分の差額を支払う。
要するに基準点、切り込み1、切り込み2の3点を円周上にランダムに配置しているだけなのです。その位置は
一様分布(連続)に従っていて、範囲は

[度]になっているというわけ。
3点をデタラメにばら撒いているだけなので、どっちに基準点が入るかは5分5分のような気がする。ならば勝敗は5分5分なんでしょうか?

[スタート]ボタンをクリックするとリングが回転します。その後、同じボタン([最初の切り込み]となっている)をクリックすると赤い三角形の箇所に切り込みが入り、更に同じボタン([次の切り込み]となっている)をクリックすると2箇所目に切り込みが入ってリングは停止します。
あなたの取り分が緑色で示されます。あなたは見事勝利することができるでしょうか?勝率や成績を調べてみてくださいね(果たして5分5分?)。
が素数
で割れる確率は、
であるというのは分かりますか?
となります。つまり全自然数の3つに1つが素数3で割れる自然数だということになります。
パッと選んだ自然数が3で割れるかは3つに1つ、つまり確率1/3となります。
で割れる確率は
となります。
と
がどちらも素数
で割れる確率は
となります。
と
が素数
を公約数に持たない確率は
となります。
と
が互いに素ということはあらゆる素数が公約数でないということなので、その確率は
という部分は「バーゼル問題」という数学の歴史的難問(解決に100年!)に端を発し、数学の最大の未解決問題とされる「リーマン予想」にも関わるネタで、
とてもここでは書ききれません。
 RSS
RSS

