特異値分解入門(3)

May 22, 2010

不正な相関行列 ${\boldsymbol C}$ が与えられると何が起きるが考えてみましょう。
前回の解説の “事実3” で悲劇が起きます。つまり、

${\small \begin{pmatrix}\lambda_1&0&\cdots&0\\0&\lambda_2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\lambda_{N}\end{pmatrix}=\begin{pmatrix}\sqrt{\lambda_1}&0&\cdots&0\\0&\sqrt{\lambda_2}&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sqrt{\lambda_{N}}\end{pmatrix}\begin{pmatrix}\sqrt{\lambda_1}&0&\cdots&0\\0&\sqrt{\lambda_2}&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sqrt{\lambda_{N}}\end{pmatrix}}$

とする時になって、ハッと気が付くのです…「固有値が負だ！」と。
そしてコンピューターは無情にも「負の平方根は計算できません」というメッセージを残して息絶えます。
ちなみに第1回に載せた不正な相関行列、

${\boldsymbol C}=\begin{pmatrix}1&1&-1\\1&1&1\\-1&1&1\end{pmatrix}$

の固有値は $-1,2,2$ となります。

この困難を打破してとにかく答えを出したい！そこでいよいよ特異値分解の登場です。

先ずは特異値分解で任意の行列（なんと正方行列でなくてもいい！） ${\boldsymbol A}$ はどのように分解されるか見てみましょう。

${\boldsymbol A}={\boldsymbol U}{\boldsymbol W}{\boldsymbol V}^\text{t}$

となります。とりあえずここでは ${\boldsymbol A}$ として実対称正方行列であるところの相関行列 ${\boldsymbol C}$ だけを対象にして順に説明していきましょう。

行列 ${\boldsymbol C}$ から ${\boldsymbol M}={\boldsymbol C}{\boldsymbol C}^\text{t}$ なる行列を計算します。この行列は自動的に、

正方行列
対称行列
半正定値行列

となるんです！（もちろんもとの行列が実数の行列ならば ${\boldsymbol M}$ も実数）。最後の特徴に注目してください。簡単に言うと、元の行列（ ${\boldsymbol C}$ ）2乗することで負だった固有値があったとしてもそれが正になるということです。
というわけで行列 ${\boldsymbol M}$ は互いに直交する固有ベクトルを持ち、固有値は全て0以上となります。この固有ベクトルを並べた行列が ${\boldsymbol U}$ です。
次に、 ${\boldsymbol N}={\boldsymbol C}^\text{t}{\boldsymbol C}$ なる行列を作ります。この行列は ${\boldsymbol M}$ の場合と全く同様に

正方行列
対称行列
半正定値行列

となります。 ${\boldsymbol N}$ の固有ベクトルを並べた行列が ${\boldsymbol V}$ です。
最後に ${\boldsymbol W}$ は行列 ${\boldsymbol C}$ の固有値の絶対値を対角に並べた対角行列になります。

ここまでの手順で分かるように、各行列 ${\boldsymbol U}$ 、 ${\boldsymbol V}$ 、 ${\boldsymbol W}$ は元の行列 ${\boldsymbol C}$ がどんなものであれ安定的に得ることができます（計算は止まらない！）。前にも述べましたがこれが最も重要な点です。

とにもかくにも行列 ${\boldsymbol C}$ は、

${\boldsymbol C}={\boldsymbol U}{\boldsymbol W}{\boldsymbol V}^\text{t}$

という形に分解されました。次に

${\small {\boldsymbol W}=\begin{pmatrix}|\lambda_1|&0&\cdots&0\\0&|\lambda_2|&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&|\lambda_{N}|\end{pmatrix}=\begin{pmatrix}\sqrt{|\lambda_1|}&0&\cdots&0\\0&\sqrt{|\lambda_2|}&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sqrt{|\lambda_{N}|}\end{pmatrix}\begin{pmatrix}\sqrt{|\lambda_1|}&0&\cdots&0\\0&\sqrt{|\lambda_2|}&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sqrt{|\lambda_{N}|}\end{pmatrix}}={\boldsymbol W}^\prime {\boldsymbol W}^\prime$

とします（対角成分は固有値の絶対値なので安心して平方根がとれる）。すると、

${\boldsymbol C}={\boldsymbol U}{\boldsymbol W}{\boldsymbol V}^\text{t}={\boldsymbol U}{\boldsymbol W}^\prime {\boldsymbol W}^\prime {\boldsymbol V}^\text{t}={\boldsymbol U}{\boldsymbol W}^\prime({\boldsymbol V}{\boldsymbol W}^\prime)^\text{t}$

となります。

あと一息です

さてここで行列 ${\boldsymbol C}$ が正しい相関行列、つまり半正定値だとどうなるか。その場合は ${\boldsymbol U}={\boldsymbol V}$ となって特異値分解は前回の解説の結果と同じになります。つまり ${\boldsymbol Q}={\boldsymbol V}{\boldsymbol W}^\prime$ とすることで、相関行列は ${\boldsymbol C}={\boldsymbol Q}{\boldsymbol Q}^\text{t}$ となって目標達成です。
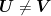
しかしそうでない場合はどうでしょう。その場合もやはり同じく ${\boldsymbol Q}={\boldsymbol V}{\boldsymbol W}^\prime$ とすることで手をうちませんか？もちろんこの場合は ${\boldsymbol C}\neq {\boldsymbol Q}{\boldsymbol Q}^\text{t}$ ではありますが（ ${\boldsymbol U}\neq{\boldsymbol V}$ だから）…でも、

安定的に答えが出る
正しい相関行列の場合は正しい答えが出る

という望ましい性質を持ってます。
因みに正しい相関行列ではない場合にも、 ${\boldsymbol Q}{\boldsymbol Q}^\text{t}$ の各成分の符号は元の行列 ${\boldsymbol C}$ のそれに等しくなります（正の相関が負になることはない）。

再び

${\boldsymbol C}=\begin{pmatrix}1&1&-1\\1&1&1\\-1&1&1\end{pmatrix}$

を例に計算してみましょう。特異値分解の結果は、

${\boldsymbol C}=\underbrace{\begin{pmatrix}0.577&-0.739&-0.348\\-0.577&-0.671&0.466\\0.577&0.068&0.814\end{pmatrix}}_{{\boldsymbol U}}\underbrace{\begin{pmatrix}1&0&0\\0&2&0\\0&0&2\end{pmatrix}}_{{\boldsymbol W}^\prime}\underbrace{\begin{pmatrix}-0.577&0.577&-0.577\\-0.739&-0.671&0.068\\-0.348&0.466&0.814\end{pmatrix}}_{{\boldsymbol V}^\text{t}}$

となります（ ${\boldsymbol U}\neq {\boldsymbol V}$ であることが分かりますか？第1固有ベクトルの符号が逆転しています！こうすることで、固有値の方を正に揃えているという訳です）。そして、

${\boldsymbol Q}=\underbrace{\begin{pmatrix}-0.577&-0.739&-0.348\\0.577&-0.671&0.466\\-0.577&0.068&0.814\end{pmatrix}}_{\boldsymbol V}\underbrace{\begin{pmatrix}1&0&0\\0&\sqrt{2}&0\\0&0&\sqrt{2}\end{pmatrix}}_{{\boldsymbol W}^\prime}}$