// ホーム / 資料 / 分布関数の世界 / ジョンソン SU 分布

ジョンソン SU 分布(Johnson SU distribution)NtRand Supported

正規分布の進化形ジョンソン SU 分布

最近、正規分布によるモデルに限界を感じていませんか？
政治、経済、自然…。変化の著しい今の世の中をモデル化するには、正規分布には荷が重すぎます。それは完全な左右対称性と裾の薄さという最大の弱点があるからなのです。
ジョンソン SU 分布はこれらの欠陥をカバーする分布として最近注目を浴びてきています。
この分布は歪度（分布の非対称性）と尖度（裾の厚さ）を適当に与えることで分布の形状をかなり自由に操作できるという特徴をもっているのです。

分布の形状

基本情報

  • 4つのパラメータ \gamma, \delta,\lambda,\xi が必要です (どうやって求めるの？).
    \delta>0,\lambda>0
  • 無限区間 (-\infty,+\infty) で定義された連続分布.
  • 平均対して対称にも非対称にもなり得ます。

確率

  • 累積分布関数
    F(x)=\Phi\left(\gamma+\delta\sinh^{-1}z\right)
    ここで
    z=\frac{x-\xi}{\lambda}
    で、\Phi(\cdot) は標準席分布の累積分布関数です。
  • 確率密度関数
    f(x)=\frac{\delta}{\lambda\sqrt{2\pi}\sqrt{z^2+1}}\exp\left[-\frac{1}{2}\left(\gamma+\delta\sinh^{-1}z\right)^2\right]
  • Excel での累積分布関数 (c.d.f.) と 確率密度関数 (p.d.f.)の求め方
     
    1
    2
    3
    4
    5
    6
    7
    8
       
    9
       
    AB
    データ説明
    2.5 対象となる値
    1 分布のパラメータ Gamma の値
    4 分布のパラメータ Delta の値
    3 分布のパラメータ Lambda の値
    0.9 分布のパラメータ Xi の値
    数式説明（計算結果）
    =NTJOHNSONSUDIST(A2,A3,A4,A5,A6,TRUE) 上のデータに対する累積分布関数の値
    =NTJOHNSONSUDIST(A2,A3,A4,A5,A6,FALSE) 上のデータに対する確率密度関数の値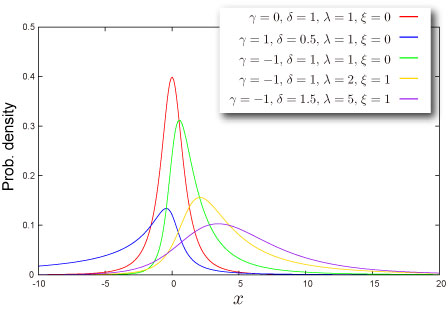
    Sample distribution
  • 関連 NtRand 関数 : NTJOHNSONSUDIST

分位点

  • 累積分布関数の逆関数
    F^{-1}(P)=\lambda\sinh\left(\frac{\Phi^{-1}(P)-\gamma}{\delta}\right)+\xi
    ここで \Phi(\cdot) は 標準正規分布の累積分布関数です。.
  • Excel での分位点の求め方
     
    1
    2
    3
    4
    5
    6
    7
    8
       
    AB
    データ説明
    0.5 上のデータに対する確率密度関数の値
    1 分布のパラメータ Gamma の値
    4 分布のパラメータ Delta の値
    3 分布のパラメータ Lambda の値
    0.9 分布のパラメータ Xi の値
    数式説明（計算結果）
    =NTJOHNSONSUINV(A2,A3,A4,A5,A6) 上のデータに対する累積分布関数の逆関数の値
  • 関連 NtRand 関数 : NTJOHNSONSUINV

分布の特徴

平均 – 分布の”中心”はどこ？ (定義)

  • 分布の平均 は次式で与えられます。
    \xi-\lambda\omega^{1/2}\sinh\Omega
    ここで
    \omega=\exp\left(\delta^{-2}\right),\;\Omega=\gamma/\delta
    です。
  • Excel での計算法
     
    1
    2
    3
    4
    5
    6
    7
    AB
    データ説明
    1 分布のパラメータ Gamma の値
    4 分布のパラメータ Delta の値
    3 分布のパラメータ Lambda の値
    0.9 分布のパラメータ Xi の値
    数式説明（計算結果）
    =NTJOHNSONSUMEAN(A2,A3,A4,A5) 上のデータに対す分布の平均
  • 関連 NtRand 関数 : NTJOHNSONSUMEAN

標準偏差 – 分布はどのくらい広がっているか（定義）

  • 分布の分散 は次式で与えられます。
    \frac{\lambda^2}{2}(\omega-1)(\omega\cosh 2\Omega+1)
    ここで
    \omega=\exp\left(\delta^{-2}\right),\;\Omega=\gamma/\delta
    です。

    標準偏差 は 分散の正の平方根です。

  • Excel での計算法
     
    1
    2
    3
    4
    5
    6
    7
    AB
    データ説明
    1 分布のパラメータ Gamma の値
    4 分布のパラメータ Delta の値
    3 分布のパラメータ Lambda の値
    0.9 分布のパラメータ Xi の値
    数式説明（計算結果）
    =NTJOHNSONSUSTDEV(A2,A3,A4,A5) 上のデータに対する分布の標準偏差
  • 関連 NtRand 関数 : NTJOHNSONSUSTDEV

歪度 – 分布はどちらに偏っているか(定義)

  • 分布の歪度 は次式の平方根で与えられます。
    \beta_1=\omega(\omega-1)\frac{[\omega(\omega+2)\sinh 3\Omega+3\sinh\Omega]^2}{2(\omega\cosh 2\Omega+1)^3}
    ここで
    \omega=\exp\left(\delta^{-2}\right),\;\Omega=\frac{\gamma}{\delta}
    です。歪度の符号は、\Omegaの符号の逆です。
  • Excel での計算法
     
    1
    2
    3
    4
    5
    6
    7
    AB
    データ説明
    1 分布のパラメータ Gamma の値
    4 分布のパラメータ Delta の値
    3 分布のパラメータ Lambda の値
    0.9 分布のパラメータ Xi の値
    数式説明（計算結果）
    =NTJOHNSONSUSKEW(A2,A3,A4,A5) 上のデータに対する分布の歪度
  • 関連 NtRand 関数 : NTJOHNSONSUSKEW

尖度 – 尖っているか丸まっているか (定義)

  • 分布の尖度 は次式で与えられます。
    \beta_2=\frac{\omega^2(\omega^4+2\omega^3+3\omega^2-3)\cosh 4\Omega+4\omega^2(\omega+2)\cosh 2\Omega+3(2\omega+1)}{2(\omega\cosh 2\Omega+1)^2}-3
    ここで
    \omega=\exp\left(\delta^{-2}\right),\;\Omega=\frac{\gamma}{\delta}
    です。
  • Excel での計算法
     
    1
    2
    3
    4
    5
    6
    7
    AB
    データ説明
    1 分布のパラメータ Gamma の値
    4 分布のパラメータ Delta の値
    3 分布のパラメータ Lambda の値
    0.9 分布のパラメータ Xi の値
    数式説明（計算結果）
    =NTLOGNORMKURT(A2,A3,A4,A5) 上のデータに対する分布の尖度
  • 関連 NtRand 関数 : NTJOHNSONSUKURT

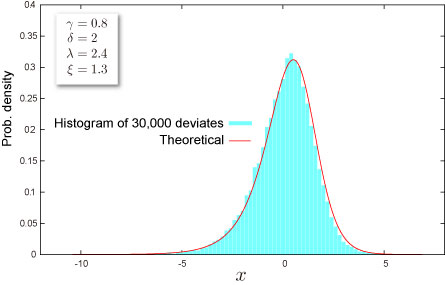
乱数

  • 乱数 x は一様乱数 U に対して次式で生成されます（逆関数法） :
    x=\lambda\sinh\left(\frac{\Phi^{-1}(U)-\gamma}{\delta}\right)+\xi
  • Excel での乱数生成法
     
    1
    2
    3
    4
    5
    6
    7
       
    AB
    データ説明
    1 分布のパラメータ Gamma の値
    4 分布のパラメータ Delta の値
    3 分布のパラメータ Lambda の値
    0.9 分布のパラメータ Xi の値
    数式説明（計算結果）
    =NTRANDJOHNSONSU(100,A2,A3,A4,A5,0) 100個のジョンソン SU 乱数を Mersenne Twister アルゴリズムで生成します。

    メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A5:A104 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

関連 NtRand 関数

参照

 

Comments are closed.